On a pour objectif de calculer numériquement une intégrale. Pour cela, nous allons introduire les polynômes d’interpolation de Lagrange. Nous allons définir les notions de formule de quadrature, de formule de quadrature exactes sur des espaces polynomiaux. Enfin on définira les formules ou méthodes de Newton-Cotes et les cas particuliers des formules composites des rectangles, des trapèzes et de Simpson

Soit $f:[a,b] \rightarrow \mathbf{R}$ une fonction continue. L’objectif est de calculer l’intégrale suivante:

\[I(f)=\int_a^bf(x)dx\]

On partitionne l’intervalle $[a,b]$ en $n$ intervalles $[x_i,x_{i+1}],i=0,\ldots,n-1$ avec

\[a = x_{0} < x_{1} < \ldots < x_{n} =b.\]

On a alors:

\[I(f)=\int_a^bf(x)dx=\sum_{i=0}^{n-1}\int_{x_i}^{x_{i+1}}f(x)dx\]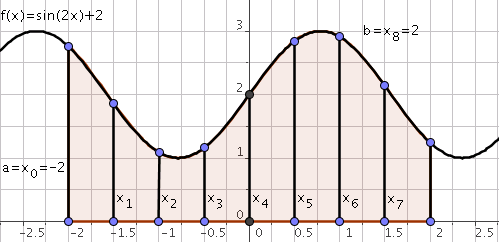

On doit donc déterminer l’intégrale suivante:

\[\int_{x_i}^{x_{i+1}}f(x)dx,i=0,\ldots,n-1.\]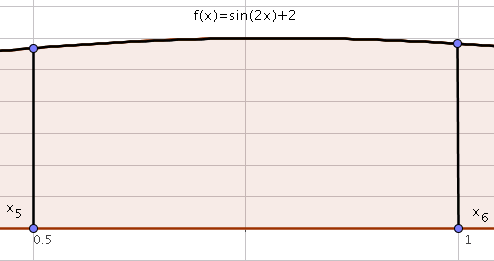

En se ramenant sur l’intervalle $[-1,1]$ via le changement de variable

\[t=2\frac{x-x_{i}}{x_{i+1}-x_{i}}-1\]

ou encore

\[x=\frac{x_{i+1}-x_{i}}{2}(t+1)+x_i\]

d’où

\[\int_{x_i}^{x_{i+1}}f(x)dx=\frac{x_{i+1}-x_{i}}{2} \int_{-1}^{1}g_i(t)dt\]

avec

\[g_i(t)=f\left(\frac{x_{i+1}-x_{i}}{2}(t+1)+x_i\right),i=0,\ldots,n-1.\]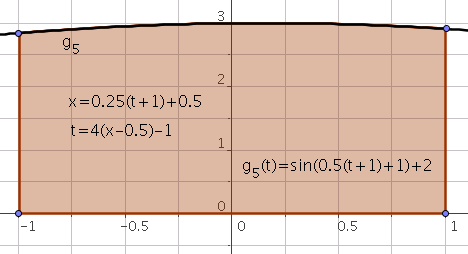

Formule de quadrature

Soit $g$ une fonction continue sur $[-1,1]$. On appelle formule de quadrature l’application $J$ définie par:

\[J:g \longmapsto \sum_{j=0}^p\omega_j g(t_j)\]

les points:

\(-1\leq t_0 < t_1 < \ldots < t_p \leq 1\) sont appelés points d’intégration de la formule de quadrature $J$ et \(\omega_0,\omega_1,\ldots,\omega_p\) sont les poids de la formule de quadrature $J$.

Les poids et les points d’intégration sont choisis de telle manière que:

\[\int_{-1}^{1}g(t)dt\simeq\sum_{j=0}^p\omega_j g(t_j)\]

Formule de quadrature exacte

Soit $Q\in\mathbf{P}_q$, l’ensemble des polynomes de degré inférieur ou égal à $q$. La formule de quadrature $J$ est dite exacte sur $\mathbf{P}_q$, si

\[\forall Q\in\mathbf{P}_q,\quad \int_{-1}^{1}Q(t)dt=J(Q)\]

c’‘est à  dire

\[\forall Q\in\mathbf{P}_q,\quad \int_{-1}^{1}Q(t)dt=\sum_{j=0}^p\omega_j Q(t_j)\]

Formule de quadrature exacte: base de Lagrange

Théorème.

Soit $L_0,L_1,\ldots,L_p$ la base de Lagrange de $\mathbf{P}_{p}$ relativement aux points \(-1 \leq t_0 < t_1 < \ldots < t_p \leq 1.\)

On a l’équivalence suivante:

\[J(g)=\sum_{j=0}^p\omega_j g(t_j)\mbox{ exacte sur } \mathbf{P}_{p} \Longleftrightarrow \omega_j=\int_{-1}^{1}L_j(t)dt,\quad j=0,1,\ldots,p.\]

Formule de Newton-Cotes

On appelle méthode de Newton-Cotes les méthodes précédentes pour lesquelles on choisit des points $(x_i)_{i=0,\ldots,n}$ équidistants:

\[x_i=x_0+hi\]

avec $h=\frac{b-a}{n}$. Dès lors:

\[\begin{array}{ccl} \displaystyle\int_{x_i}^{x_{i+1}}f(x)dx &=& \displaystyle\frac{x_{i+1}-x_{i}}{2} \int_{-1}^{1}g_i(t)dt\\ &\simeq& \displaystyle\frac{h}{2}J(g_i)\\ &\simeq& \displaystyle\frac{h}{2}\sum_{j=0}^p\omega_j g_i(t_j)\\ &\simeq& \displaystyle\frac{h}{2}\sum_{j=0}^p\omega_j f\left(\frac{h}{2}(t_j+1)+x_i\right) \end{array}\]

On peut à  présent approcher $I(f)=\int_a^bf(x)dx$ par la formule composite $I_h(f)$:

\[\begin{array}{ccl} \displaystyle I(f)=\int_a^bf(x)dx&=&\displaystyle\sum_{i=0}^{n-1}\int_{x_i}^{x_{i+1}}f(x)dx\\ &\simeq&\displaystyle\frac{h}{2}\sum_{i=0}^{n-1}\sum_{j=0}^p\omega_j f\left(\frac{h}{2}(t_j+1)+x_i\right) \end{array}\]

avec

\[I_h(f)=\frac{h}{2}\sum_{i=0}^{n-1}\sum_{j=0}^p\omega_j f\left(\frac{h}{2}(t_j+1)+x_i\right)\]

Voici quelques formules de Newton classiques ainsi que le degré $p$ de $\mathbf{P}_{p}$.

Degré p Appelation
0 Méthode des rectangles
1 Méthode des trapèzes
2 Méthode de Simpson
3 Méthode de Simpson 3/8
4 Méthode de Boole

Méthode des rectangles

La méthode des rectangles est une méthode à  1 point. On a $p=0$ et $t_0=0$. La base de Lagrange associée à  $\mathbf{P}_{0}$ est

\[L_0(t)=1\]

Par suite:

\[\omega_0=\int_{-1}^{1}L_0(t)dt=\int_{-1}^{1}dt=2\]

La formule de quadrature est alors définie par:

\[J(g)=\omega_0g(t_0)=2g(0)\]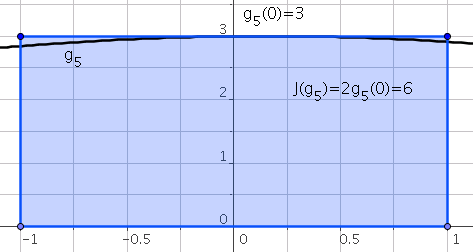

On a alors la formule composite des rectangles:

\[I_h(f)=h \sum_{i=0}^{n-1}f\left(\frac{x_i+x_{i+1}}{2}\right)\]

Méthode des trapèzes

La méthode des trapèzes est une méthode à  2 point. On a $p=1$ et $t_0=-1,t_1=1$. La base de Lagrange associée à  $\mathbf{P}_{1}$ est

\[L_0(t)=\frac{1-t}{2},L_1(t)=\frac{t+1}{2}\]

Par suite:

\[\omega_0=\int_{-1}^{1}L_0(t)dt=1;\omega_1=\int_{-1}^{1}L_1(t)dt=1\]

La formule de quadrature est alors définie par:

\[J(g)=\omega_0g(t_0)+\omega_1g(t_1)=g(-1)+g(1)\]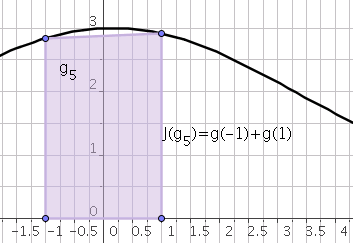

On a alors la formule composite des trapèzes:

\[I_h(f)=\frac{h}{2}\sum_{i=0}^{n-1}(f(x_i)+f(x_{i+1}))\]

Méthode de Simpson

La méthode de Simpson est une méthode à  3 point. On a $p=2$ et $t_0=-1,t_1=0,t_2=1$. La base de Lagrange associée à  $\mathbf{P}_{2}$ est

\[L_0(t)=\frac{t^2-t}{2},L_1(t)=1-t^2,L_2(t)=\frac{t^2+t}{2}\]

Par suite:

\[\omega_0=\int_{-1}^{1}L_0(t)dt=\frac{1}{3}; \omega_1=\int_{-1}^{1}L_1(t)dt=\frac{4}{3}; \omega_2=\int_{-1}^{1}L_1(t)dt=\frac{1}{3};\]

La formule de quadrature est alors définie par:

\[J(g)=\omega_0g(t_0)+\omega_1g(t_1)+\omega_2g(t_2)=\frac{1}{3}g(-1)+\frac{4}{3}g(0)+\frac{1}{3}g(1)\]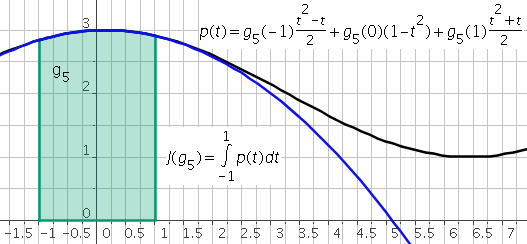

On a alors la formule composite des trapèzes:

\[I_h(f)=\frac{h}{6}\sum_{i=0}^{n-1}(f(x_i)+4 f(\frac{x_i+x_{i+1}}{2}) +f(x_{i+1}))\]