Introduction au Latex
Voici une courte introduction au Latex! Elle est destinée aux débutants, je rappelle comment les fichiers tex sont compilés et visualisés à l’aide des utilitaires xdvi et ghostview. Les principales commandes et environnement sont répertoriés. Bonne lecture !!!
Introduction
Le latex est un langage permettant de créer des documents écrits (lettre, compte-rendu, rapport, thèse, etc…). Il permet en outre d’élaborer des documents destinés aux scientifiques . De la màªme manière que le langage C, le latex est un langage compilé. Il permet d’obtenir un rendu similaire aux ouvrages scientifiques que l’on a coutume de consulter. Le Tex fut créé en 1978 par Donald E. Knuth . Son idée fut d’abord de remédier aux difficultés du monde de l’édition. Ce n’est que par la suite que d’autres chercheurs, comme Lessie Lamport, ont décidé de mettre en place des macros. Ce n’est qu’en 1982 que le métalangage LateX est né.
Fichier de base
Voici le contenu d’un fichier de base disponible ici pour débuter le LaTeX. Ouvrez un éditeur et tapez ce qui suit

- Ligne 1: c’est la classe de notre document. En l’occurence, ici c’est article dont les caractères font une taille de 12 points.
- Ligne 2: on charge le paquet latin1 avec pour option inputenc. Cela permet d’utiliser des accents, c’est le cas du français!
- Ligne 3: on charge la typographie française
- Ligne 4: on utilise l’encodage T1. Pour vulgariser cela, je dirais que cet encodage permet de palier aux glyphes manquants dans les polices PostScript!!! N’ayez pas peur !!!
- Ligne 6: ouverture du document
- Ligne 7: le contenu de notre document, à noter que la commande \Latex permet d’écrire d’écire le logo LaTeX
- Ligne 8: fermeture du document
Compilation
Nous avons vu lors de l’introduction que le latex est un langage compilé. La compilation se fait comme suit: latex nom_du_fichier.tex Par exemple :
latex base.texlorsque vous avez compilé le fichier, on obtient en sortie un fichier de màªme nom mais avec l’extension dvi. En l’occurence le fichier généré ici sera base.dvi. Pour pouvoir visionner le fichier base.dvi, on utilise le programme xdvi.
xdvi base.dvi &Néanmoins, il se peut que la compilation échoue. Cela veut dire notamment que vous vous àªtes trompés dans une des commandes latex de votre fichier. En général, si la compilation échoue, vous verrez en sortie sur votre console les numéros de lignes correspondants aux erreurs que vous avez faites. Lorsqu’une compilation a échoué, tapez x. Cela permettra d’arràªter la compilation.
Le format PostScript
Alors qu’est-ce que le PostScript ? C’est un format utilisé pour décrire les pages à une imprimante. C’est un langage opérationnel permettant de décrire aux imprimantes l’aspect graphique des pages que l’on désire imprimer. Tous les systèmes Linux, Unix et Macintosh ont pour format standard le PostScript. L’idée à présent est de construire un fichier PostScript à partir du fichier dvi générés par latex. Pour cela nous allons utiliser la commande dvips.
dvips base.dvi -ole résultat obtenu dans la console indique le nombre de pages de votre fichier PostScript. La commande - o permet de générer directement les fichiers PostScript base.ps . Si vous désirez obtenir un nom de fichier différent de celui base.ps, alors tapez :
dvips -o intro.ps base.dviPour afficher les fichiers de format PostScript, on utilise le logiciel gv (pour Ghostview). Il est appelé comme suit :
ghostview base.ps &en pratique si on veut imprimer un fichier PostScript, on procède comme suit :
lpr base.pssi l’on veut imprimer en recto verso on utilise la commande de Zdouble :
lpr -Zdouble base.psEnfin, et cela s’avère souvent utile pour l’économie de papier, on peut imprimer deux pages par feuille voir plus:
lpr -o number-up=2 fichier.psCommandes de base
Voici quelques commandes de base essentielles pour bien débuter le latex. Les commandes commencent toutes par l’antislash . Lorsque ces dernières ont des arguments, ils sont entre des accolades. Quant aux options, elles sont entre crochets et précèdent toujours les arguments:
\commande[option]{argument}
Le double antislash \ permet de forçer le passage à la ligne. Enfin le caractère $ permet d’ouvrir et de fermer le mode mathématique. Nous verrons par la suite les principaux environnements mathématiques. Voici quelques exemples de commandes de base.
| Définition | Code LaTeX | Résultat |
|---|---|---|
| Fraction | \frac{a}{b} |
$\frac{a}{b}$ |
| Multiplication | x \times y=xy |
$x \times y=xy$ |
| Indice simple | u_n |
$u_n$ |
| Indice multiple | f_{xy} |
$f_{xy}$ |
| Exposant simple | a^3 |
$a^3$ |
| Exposant multiple | x^{3a} |
$x^{3a}$ |
| Racine Carrée | \sqrt{2} |
$\sqrt{2}$ |
| Racine n-ième | \sqrt[n]{2} |
$\sqrt[n]{2}$ |
| Somme | \sum_{k=1}^{n}u_k |
$\sum_{k=1}^{n}u_k$ |
| Limite | \lim_{x \to +\infty}f(x) |
$\lim_{x \to +\infty}f(x)$ |
| Intégrale | \int_{a}^{b}f(x)\,dx |
$\int_{a}^{b}f(x)\,dx$ |
| Vecteur | \vec{u}=\vec{AB} |
$\vec{u}=\vec{AB}$ |
| Angle | \widehat{ABC} |
$\widehat{ABC}$ |
| Conjugué | \overline{z+z'} |
$\overline{z+z’}$ |
Voici un exemple d’inclusion de telles commandes:
La première identité remarquable: $(a+b)^2=a^2+2ab+b^2$.\\
On considère le repère $(O,\vec{i},\vec{j})$.\\
Montrez que la suite $u_n$ converge vers $\sqrt{\sqrt{\sqrt{\sqrt{2}}}}$.La première identité remarquable: $(a+b)^2=a^2+2ab+b^2$.
On considère le repère $(O,\vec{i},\vec{j})$.
Montrez que la suite $u_n$ converge vers $\sqrt{\sqrt{\sqrt{\sqrt{2}}}}$.
Les lettres grecques
| Symbole | Rendu | Symbole | Rendu | Symbole | Rendu | Symbole | Rendu |
|---|---|---|---|---|---|---|---|
\alpha |
$\alpha$ | \eta |
$\eta$ | \nu |
$\nu$ | \varsigma |
$\varsigma$ |
\beta |
$\beta$ | \theta |
$\theta$ | \pi |
$\pi$ | \tau |
$\tau$ |
\gamma |
$\gamma$ | \vartheta |
$\vartheta$ | \varpi |
$\varpi$ | \upsilon |
$\upsilon$ |
\delta |
$\delta$ | \iota |
$\iota$ | \rho |
$\rho$ | \phi |
$\phi$ |
\epsilon |
$\epsilon$ | \kappa |
$\kappa$ | \varrho |
$\varrho$ | \varphi |
$\varphi$ |
\varepsilon |
$\varepsilon$ | \lambda |
$\lambda$ | \sigma |
$\sigma$ | \chi |
$\chi$ |
\zeta |
$\zeta$ | \mu |
$\mu$ | \xi |
$\xi$ | \psi |
$\psi$ |
\omega |
$\omega$ | \Gamma |
$\Gamma$ | \Delta |
$\Delta$ | \Theta |
$\Theta$ |
\Lambda |
$\Lambda$ | \Xi |
$\Xi$ | \Pi |
$\Pi$ | \Sigma |
$\Sigma$ |
\Upsilon |
$\Upsilon$ | \Phi |
$\Phi$ | \Psi |
$\Psi$ | \Omega |
$\Omega$ |
Environnements
Mise en page
On présente ici quelques environnements de mise en page, notamment ceux concernant les textes justifiés. Voici quelques exemples.
\begin{flushleft}
Texte justifié à gauche
\end{flushleft}
\begin{flushright}
Texte justifié à droite
\end{flushright}
\begin{center}
Texte centré
\end{center}
Listes
Les listes ou énumérations sont couramment utilisés en LaTeX. Nous étudions ici les principales format de listes que LaTeX propose. La commande \item permet de définir une énumération. Tout d’abord l’environnement itemize, c’est l’environnement le plus utilisé dans la langue française. Chaque énumération est précedée d’un tiret.
\begin{itemize}
\item mon premier item
\item mon second item
\item mon troisième item
\end{itemize}
Quant à l’environnement , il dispose d’un compteur: chaque appel de la commande \item provoquera une incrémentation de ce compteur.
\begin{enumerate}
\item 1er
\item second
\item troisième
\end{enumerate}
Enfin, on termine par l’environnement description. Ce dernier permet de définir un attribut à chaque énumeration comme dans l’exemple suivant.
\begin{description}
\item[Nom] Soualem
\item[Prénom] Nadir
\item[Sexe] Masculin
\end{description}
Vers et Poésie …
\begin{verse}
Non pas que je sois fétichiste mais j'aime le \Latex \\
Il est la plume des scientifiques qui ne se prennent pas la tàªte,\\
Meilleur que les logiciels de Billou,\\
Il vous réjouit avant tout.
\end{verse}
Mode Verbatim
Le mode verbatim permet de voir le code tel qu’il est écrit:
\begin{verbatim}
\begin{quotation}
Le c\oe ur a ses raisons que la raison ne connaà®t pas.
\end{quotation}
\end{verbatim} 
Mode Quotation
Le mode quotation permet de faire des citations:
\begin{quotation}
Le c\oe ur a ses raisons que la raison ne connaà®t pas.
\end{quotation} 
Tableaux
En LaTeX, les tableaux sont représentés par l’environnement tabular. Le nombre de colonnes est défini après tabular entre crochets. Si on veut 3 colonnes, alors
\begin{tabular}{crl}si, on veut 7 colonnes
\begin{tabular}{crccllr}on devine clairement qu’il y a autant de colonnes que de lettres. à€ quoi correspondent les lettres l, r et c?
- l: left, le contenu de la colonne sera justifié à gauche
- r: right, le contenu de la colonne sera justifié à droite
- c: center, le contenu de la colonne sera centré.
Par défaut, notre tableau ne possède ni de bordures, ni d’intercolonnes. Pour spécifier, une bordure ou une intercolonne, on utilise dans la définition de notre environnement tabular, le séparateur |. Voici un tableau possèdant 3 colonnes. Ici ce tableau possède des bordures et des intercolonnes.
\begin{tabular}{|c|r|l|}Celui-ci que des intercolonnes:
\begin{tabular}{c|l|l}Enfin ce dernier tableau possède que des bordures:
\begin{tabular}{|crc|}On peut aussi s’amuser à mettre qu’une bordure droite:
\begin{tabular}{|llc}Une question naturelle se pose alors: comment faire des interlignes ou des bordures horizontales de tableaux? C’est au sein màªme du tableau que l’on va utiliser l’attribut \hline. La commande \hline va permettre de créer un séparateur horizontal. Enfin il faut créer des séparateurs de colonnes à chaque ligne de notre tableau. C’est le rà´le du caractère &. Si on a 3 colonnes, il faut deux séparateurs & de telle manière à disposer les éléments du tableau comme suit
élément1 & élément2 & élément3 \\le double antislash \ permet de passer à la ligne suivante. Les exemples suivants permettent mieux d’appréhender la notion de tableaux.
\begin{tabular}{|l|r|c|}
\hline
$\alpha$ & $\beta$ & $\gamma$ \\
la lettre a & la lettre b & la lettre g \\
\hline
$\xi$ & $\lambda$ & $\rho$ \\
la lettre x & la lettre l & la lettre r\\
\hline
\end{tabular}
\begin{tabular}{lrc}
\hline
$\alpha$ & $\beta$ & $\gamma$ \\
la lettre a & la lettre b & la lettre g \\
\hline
$\xi$ & $\lambda$ & $\rho$ \\
la lettre x & la lettre l & la lettre r\\
\hline
\end{tabular}
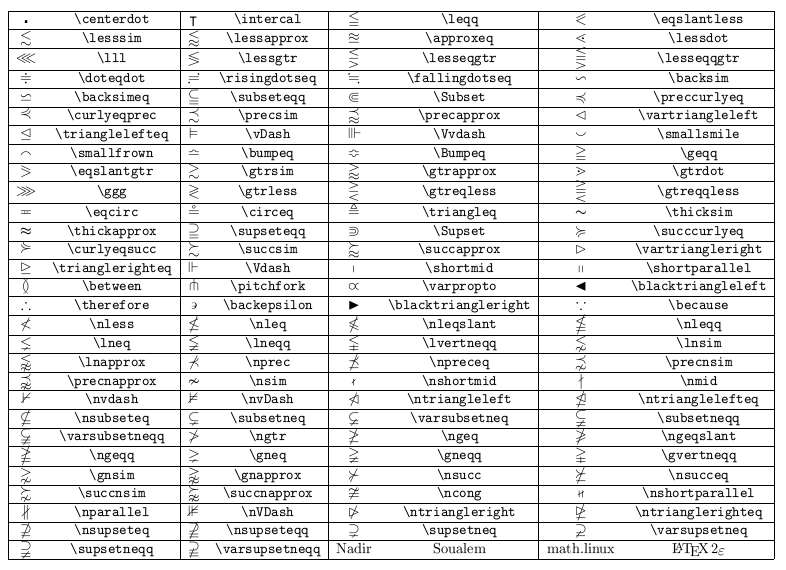
Symboles mathématiques
J’ai essayé tant bien que mal de répertorier l’ensemble des principaux symboles mathématiques les plus communément utilisés. Si un symbole important a été omis veuillez m’en excuser par avance et m’en avertir par email. A noter que pour les caractères exotiques je vous conseille vivement d’inclure les packages suivant dans votre préambule.
\usepackage{amsmath}
\usepackage{amsfonts}
\usepackage{amssymb}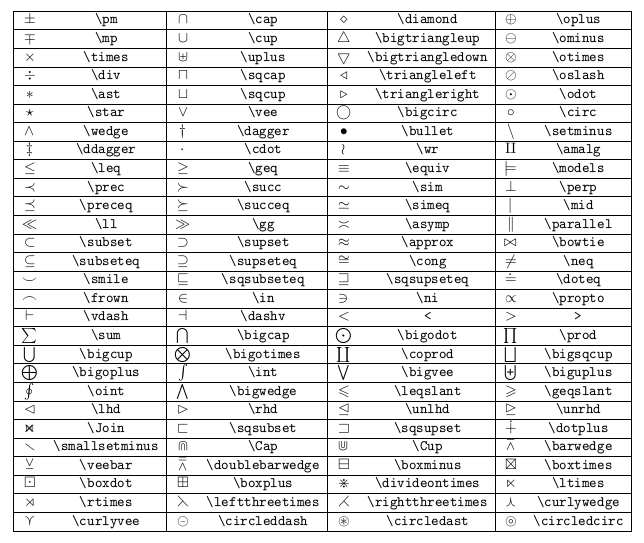
Si vous avez trouvé cet article ou ce site utile et souhaitez soutenir notre travail, veuillez envisager de faire un don. Merci !
Aidez-nousArticles dans la même rubrique
- Useful software to start LaTeX
- Introduction au Latex
- Introduction à Beamer - Faire une présentation en Latex
- How to make a presentation with Latex - Introduction to Beamer
- Latex
- /faq/
- /faq/extra/
-
/faq/latex-faq/
- Variance Symbol in LaTeX
- Union and Big Union Symbol in LaTeX
- Transpose Symbol in LaTeX
- Transformée de Laplace en LaTeX
- Texte au dessus d'une flèche en LaTeX
- Text above arrow in LaTeX
- Symbole "plus grand que ou similaire à" en LaTeX
- Symbole de Variance en LaTeX
- Symbole de transposée en LaTeX
- Symbole de "non équivalent à" en LaTeX
- Symbole d'union et de grande union en LaTeX
- Symbole d'intersection et de grande intersection en LaTeX
- Strikethrough - strike out text or formula in LaTeX
- Passer en mode mathématique en Latex: $, $$ et displaymath
- Partial Derivatives of Multivariable Functions in LaTeX
- Numéroter les équations en Latex: leqno et fleqn
- Not Equivalent Symbol in LaTeX
- Latex yen symbol
- Latex valeur absolue
- Latex tensor product
- Latex symbole sous-ensemble - inclusion
- Latex symbole racine carrée
- Latex symbole produit
- Latex symbole produit vectoriel
- Latex symbole pourcentage
- Latex symbole plus ou moins
- Latex symbole parallèle
- Latex symbole orthogonal - Latex symbole perpendiculaire
- Latex symbole norme pour un vecteur ou une somme
- Latex symbole n'existe pas
- Latex symbole n'est pas un sous-ensemble - non-inclus
- Latex symbole n'est pas parallèle
- Latex symbole n'appartient pas à
- Latex symbole multiplication
- Latex symbole loi normale
- Latex symbole infini
- Latex symbole il existe
- Latex symbole il existe un seul et unique
- Latex symbole euro
- Latex symbole Est proportionnel à
- Latex symbole espérance mathématiques
- Latex symbole équivalent / équivalence
- Latex symbole dual ou dague
- Latex symbole différent
- Latex symbole dérivée partielle
- Latex symbole degré
- Latex symbole de la moyenne
- Latex symbole de la constante de Planck h
- Latex symbole congruent
- LaTeX symbole complément
- Latex symbole chapeau
- Latex symbole approximativement
- Latex symbole appartient à
- Latex symbol there exists one and only one
- Latex symbol Planck constant h
- LaTex symbol partial derivative
- Latex symbol not in
- Latex symbol not exists
- Latex symbol not equal
- Latex symbol norm for vector and sum
- Latex symbol multiply
- LaTeX symbol Is proportional to
- Latex symbol if and only if / equivalence
- Latex symbol for all x
- Latex symbol exists
- Latex symbol different
- Latex symbol checkmark
- LaTeX symbol characteristic function
- Latex symbol belongs to
- Latex symbol average
- Latex symbol approximately
- Latex subset symbol
- Latex square root symbol
- Latex real part symbol
- Latex real numbers
- Latex rational numbers
- Latex quaternion numbers
- Latex produit tensoriel
- Latex product symbol
- Latex pour tout x
- Latex points de suspension: \ldots,\cdots,\vdots et \ddots
- Latex plus or minus symbol
- Latex piecewise function
- Latex partie réelle
- Latex partie imaginaire
- Latex parallel symbol
- Latex overset and underset
- Latex orthogonal symbol - Latex perpendicular symbol
- Latex numbering equations
- Latex not subset symbol
- Latex not parallel symbol
- Latex normal distribution symbol
- Latex natural numbers
- Latex k parmi n - coefficient binomial
- Latex jacobian symbol
- Latex infinity symbol
- Latex indicator function
- Latex imaginary part symbol
- Latex how to write underscore
- Latex how to write text in math mode
- Latex how to write percent
- Latex how to write bar
- Latex how to write a fraction
- Latex how to insert a blank or empty page with or without numbering \thispagestyle,\newpage,\usepackage{afterpage}
- Latex how to hide page number
- Latex horizontal space: qquad,hspace, thinspace,enspace
- Latex hat symbol - wide hat symbol
- Latex gradient symbol
- Latex fonction plancher - Latex partie entière inférieure
- Latex fonction plafond - Latex partie entière supérieure
- Latex fonction indicatrice
- Latex floor function
- Latex flèche
- Latex expected value symbol - expectation
- Latex euro symbol
- Latex espace horizontal: qquad,hspace, thinspace,enspace
- Latex ensemble vide
- Latex empty set
- Latex écrire du texte dans les équations ou en mode mathématique
- Latex dérivée, limite, somme, produit et intégrale
- LateX Derivatives, Limits, Sums, Products and Integrals
- Latex degree symbol
- Latex dagger symbol or dual symbol
- Latex copyright, trademark, registered symbols
- Latex convolution symbol
- Latex congruent symbol
- Latex complex numbers
- Latex complement symbol
- Latex comment insérer une page blanche,vide avec ou sans numéro, \thispagestyle,\newpage,\usepackage{afterpage}
- Latex comment faire un underscore
- Latex ceiling function
- Latex bra ket notation
- Latex binomial coefficient
- Latex barrer du texte ou une équation
- Latex backslash symbol
- Latex arrows
- Latex accolades horizontales et verticales: \left\{,\right\},\underbrace{} et \overbrace{}
- Latex absolute value
- Laplace Transform in LaTeX
- $L^1$, $L^2$, $L^p$ and $L^\infty$ spaces in Latex
- Intersection and big intersection symbols in LaTeX
- How to write table in Latex ? begin{tabular}...end{tabular}
- How to write number sets N Z D Q R C with Latex: \mathbb, amsfonts and \mathbf
- How to write matrices in Latex ? matrix, pmatrix, bmatrix, vmatrix, Vmatrix
- How to write angle in latex langle, rangle, wedge, angle, measuredangle, sphericalangle
- How to write algorithm and pseudocode in Latex ?\usepackage{algorithm},\usepackage{algorithmic}
- How to write a vector in Latex ? \vec,\overrightarrow
- How to get dots in Latex \ldots,\cdots,\vdots and \ddots
- How to display formulas inside a box or frame in Latex ? \boxed
- Horizontal and vertical curly Latex braces: \left\{,\right\},\underbrace{} and \overbrace{}
- Greater Than or Similar To Symbol in LaTeX
- Fonction caractéristique en LaTeX
- Espaces $L^1$, $L^2$, $L^p$ et $L^\infty$ en Latex
- Écrire les ensembles classiques en Latex: \mathbb, amsfonts et \mathbf
- Dérivées partielles de fonctions à plusieurs variables en LaTeX
- Comment faire un tableau en Latex ? begin{tabular}...end{tabular}
- Comment encadrer des formules en Latex ? \boxed
- Comment écrire un angle en latex langle, rangle, wedge, angle, measuredangle, sphericalangle
- Comment écrire un algorithme en Latex ?\usepackage{algorithm},\usepackage{algorithmic}
- Comment écrire des vecteurs en Latex? \vec,\overrightarrow
- Latex FAQ