Como provar que o limite de sin x / x = 1 à medida que x se aproxima de 0?

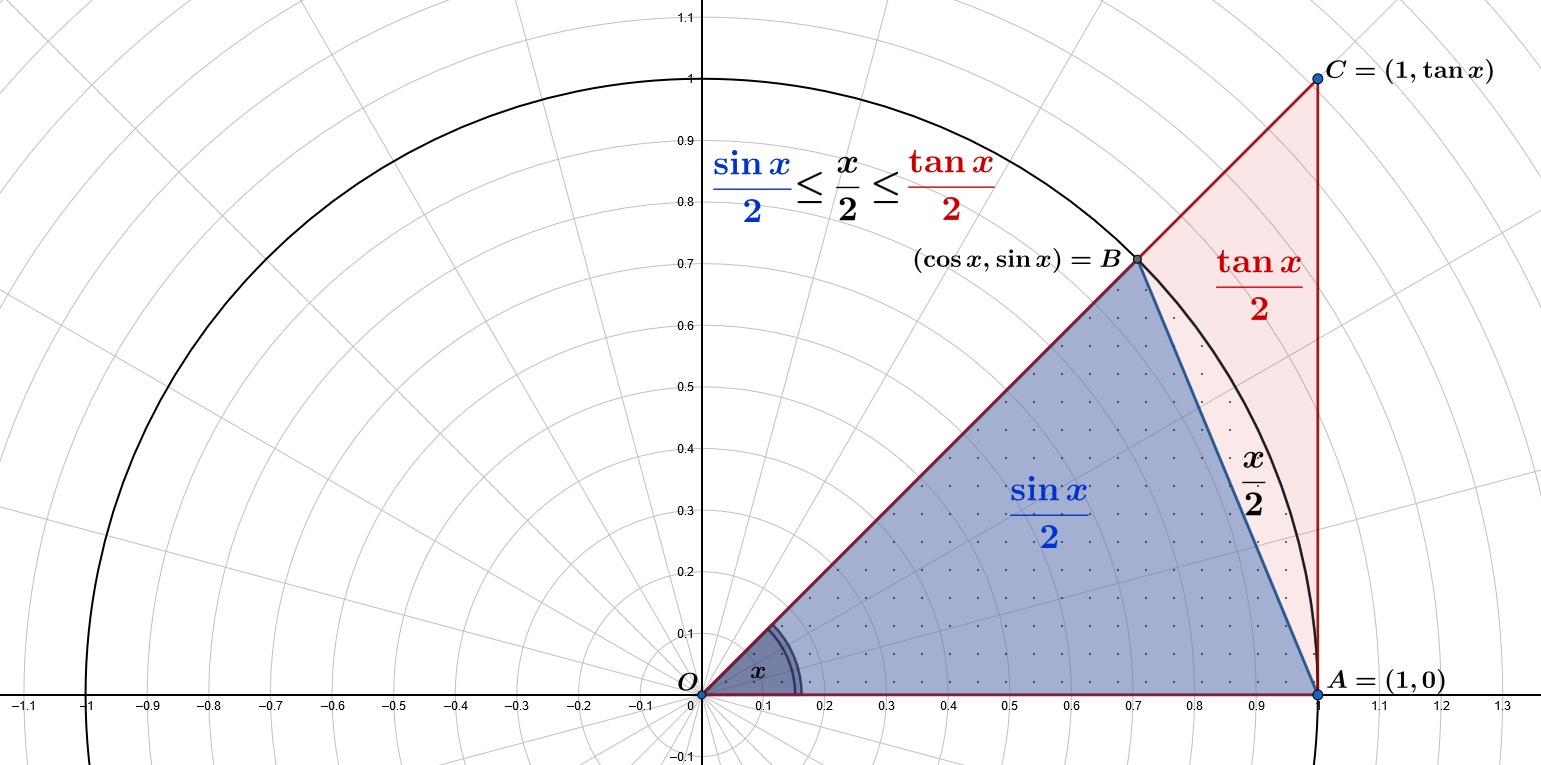
A área do pequeno triângulo azul $\color{blue}{OAB}$ é $\displaystyle A(\color{blue}{OAB})=\frac{1\cdot\sin x}{2}=\color{blue}{\frac{\sin x}{2}}$

A área do setor com pontos é $\displaystyle\pi\frac{x}{2\pi}=\frac{x}{2}$

A área do grande triângulo vermelho $\color{red}{OAC}$ é $\displaystyle A(\color{red}{OAC})=\frac{1\cdot\tan x}{2}=\color{red}{\frac{\tan x}{2}}$

Então, temos $\displaystyle A(OAB) \leq \frac{x}{2} \leq A(OAC)$:

\[0\lt \sin x \leq x \leq \tan x, \quad\displaystyle\forall x \in ]0, \frac{\pi}{2}[\]

Como $0\lt \sin x$, temos \(\begin{aligned} \frac{\sin x}{\sin x} &\leq \frac{x}{\sin x} \leq \frac{\tan x}{\sin x}\\ 1&\leq \frac{x}{\sin x} \leq \frac{1}{\cos x}\\ \end{aligned}\)

Tomando o recíproco:

\[\cos x \leq \frac{\sin x}{x} \leq 1\]

Como as funções $\displaystyle \cos x, \frac{\sin x}{x},1$ são pares, concluímos que:

\[\quad\cos x \leq \frac{\sin x}{x} \leq 1, \quad \displaystyle\forall x \in ]-\frac{\pi}{2}, 0[ \cup ]0, \frac{\pi}{2}[\]

Usando o Teorema do confronto:

\[\lim _{x \rightarrow 0} \frac{\sin x}{x}= \lim _{x \rightarrow 0} \cos x=\lim _{x \rightarrow 0} 1 = 1\]

concluímos que:

\[\lim _{x \rightarrow 0} \frac{\sin x}{x} = 1\]