当x趋近于0时证明sin x / x的极限等于1

如何证明当x趋近于0时sin x / x的极限等于1？

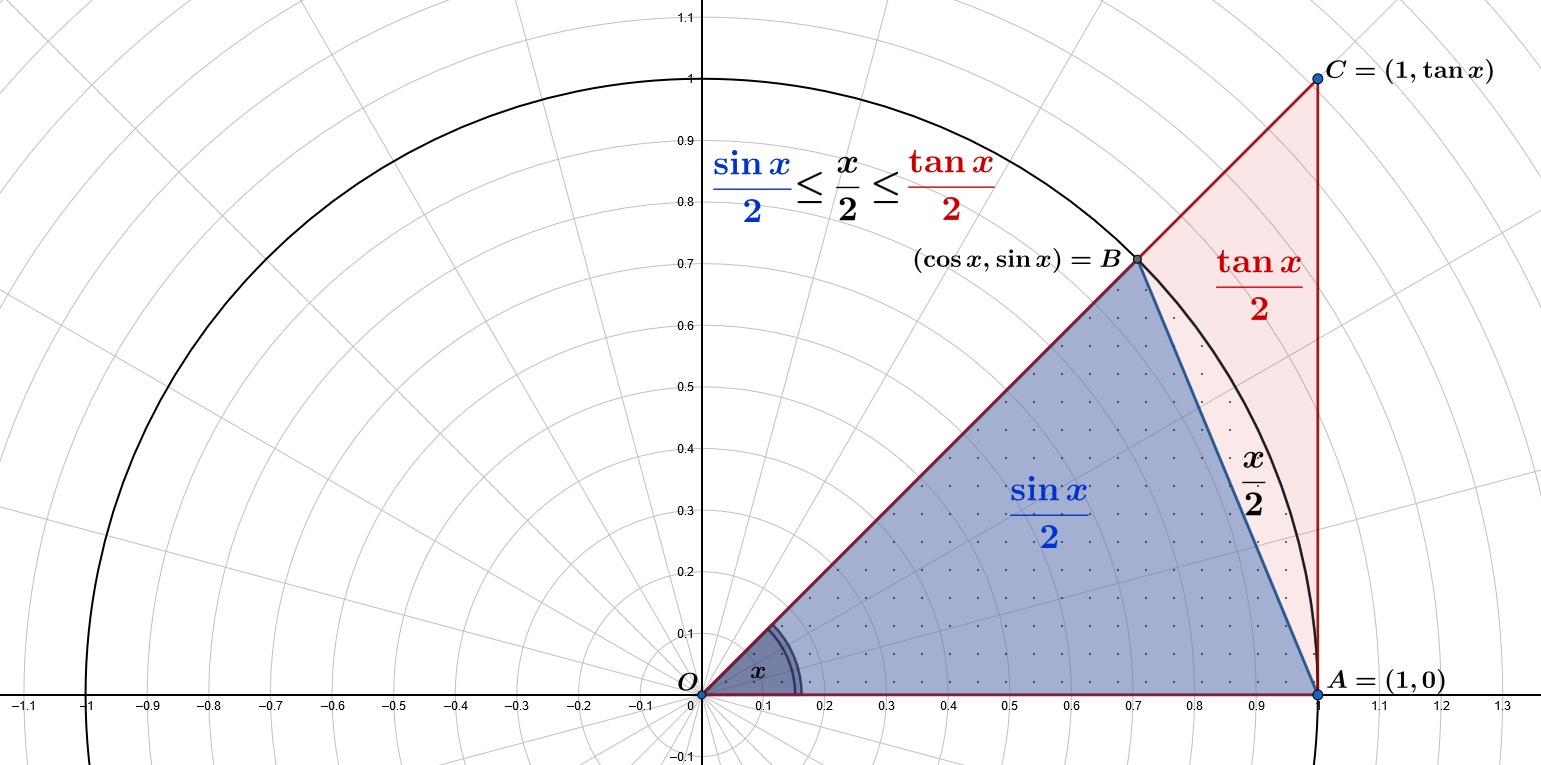
蓝色小三角形$OAB$的面积是${\displaystyle A(OAB)=\frac{1\cdot \sin x}{2}=\frac{\sin x}{2}}$

带有点的扇形的面积是${\displaystyle \pi \frac{x}{2\pi }=\frac{x}{2}}$

红色大三角形$OAC$的面积是${\displaystyle A(OAC)=\frac{1\cdot \tan x}{2}=\frac{\tan x}{2}}$

然后，我们有${\displaystyle A(OAB)\le \frac{x}{2}\le A(OAC)}$：

$$0<\sin x\le x\le \tan x,{\displaystyle \mathrm{\forall }x\in ]0,\frac{\pi }{2}[}$$

由于$0<\sin x$，我们有 $\begin{array}{rl}\frac{\sin x}{\sin x}& \le \frac{x}{\sin x}\le \frac{\tan x}{\sin x}\\ 1& \le \frac{x}{\sin x}\le \frac{1}{\cos x}\end{array}$

取倒数：

$$\cos x\le \frac{\sin x}{x}\le 1$$

由于${\displaystyle \cos x,\frac{\sin x}{x},1}$函数都是偶函数，因此我们得出结论：

$$\cos x\le \frac{\sin x}{x}\le 1,{\displaystyle \mathrm{\forall }x\in ]-\frac{\pi }{2},0[\cup ]0,\frac{\pi }{2}[}$$

通过使用夹逼定理：

$$\underset{x\to 0}{lim}\frac{\sin x}{x}=\underset{x\to 0}{lim}\cos x=\underset{x\to 0}{lim}1=1$$

我们得出结论：

$$\underset{x\to 0}{lim}\frac{\sin x}{x}=1$$