x যখন শূন্যে অবস্থানে পৌঁছে, তখন sin x / x এর সীমা হল 1 এর প্রমাণ কীভাবে করতে হয়?

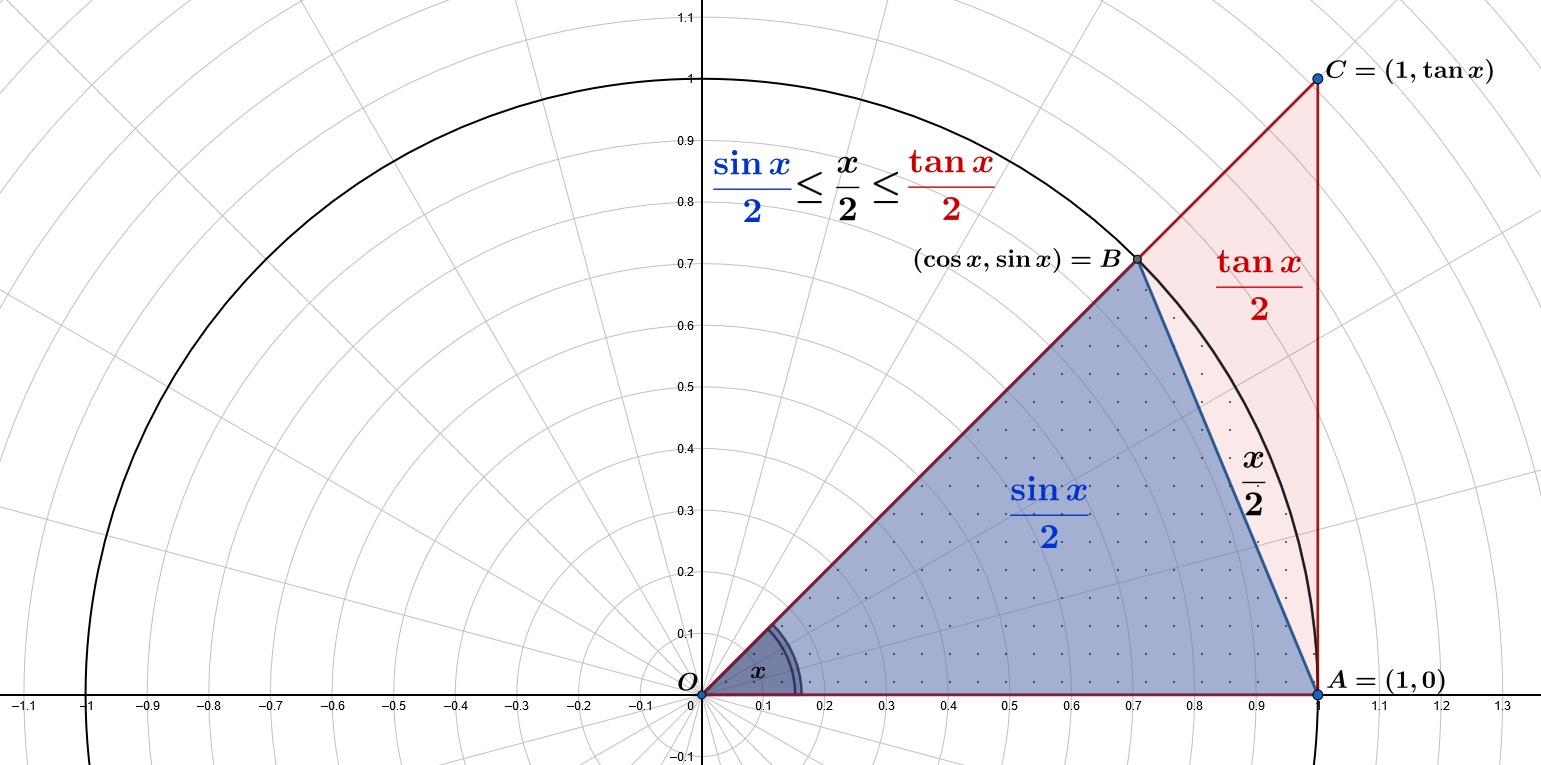
এই ছবির নীল ছোট ত্রিভুজ $\color{blue}{OAB}$ এর ক্ষেত্রফল হল $\displaystyle A(\color{blue}{OAB})=\frac{1\cdot\sin x}{2}=\color{blue}{\frac{\sin x}{2}}$

এই বিন্দুসহ সেক্টরের ক্ষেত্রফল হল $\displaystyle\pi\frac{x}{2\pi}=\frac{x}{2}$

এবং এই লাল বড় ত্রিভুজ $\color{red}{OAC}$ এর ক্ষেত্রফল হল $\displaystyle A(\color{red}{OAC})=\frac{1\cdot\tan x}{2}=\color{red}{\frac{\tan x}{2}}$

তারপর, আমরা পেতে $\displaystyle A(OAB) \leq \frac{x}{2} \leq A(OAC)$:

\[0\lt \sin x \leq x \leq \tan x, \quad\displaystyle\forall x \in ]0, \frac{\pi}{2}[\]

যেহেতু $0\lt \sin x$ আছে, তাদের জন্য আমরা লেখতে পারি \(\begin{aligned} \frac{\sin x}{\sin x} &\leq \frac{x}{\sin x} \leq \frac{\tan x}{\sin x}\\ 1&\leq \frac{x}{\sin x} \leq \frac{1}{\cos x}\\ \end{aligned}\)

যখন আমরা এদের উল্টাপেলে নেই:

\[\cos x \leq \frac{\sin x}{x} \leq 1\]

কারণ $\displaystyle \cos x, \frac{\sin x}{x},1$ এই ফাংশনগুলি সব জন্য সমস্যা, আমরা নেওয়ার দিকে পৌঁছাতে:

\[\quad\cos x \leq \frac{\sin x}{x} \leq 1, \quad \displaystyle\forall x \in ]-\frac{\pi}{2}, 0[ \cup ]0, \frac{\pi}{2}[\]

স্কুইজ থিওরি ব্যবহার করে:

\[\lim _{x \rightarrow 0} \frac{\sin x}{x}= \lim _{x \rightarrow 0} \cos x=\lim _{x \rightarrow 0} 1 = 1\]

তাহলে আমরা পেতে:

\[\lim _{x \rightarrow 0} \frac{\sin x}{x} = 1\]