x가 0에 접근할 때, sin x / x의 극한이 1임을 증명
x가 0에 접근할 때, sin x / x의 극한이 1임을 어떻게 증명할 수 있을까요?
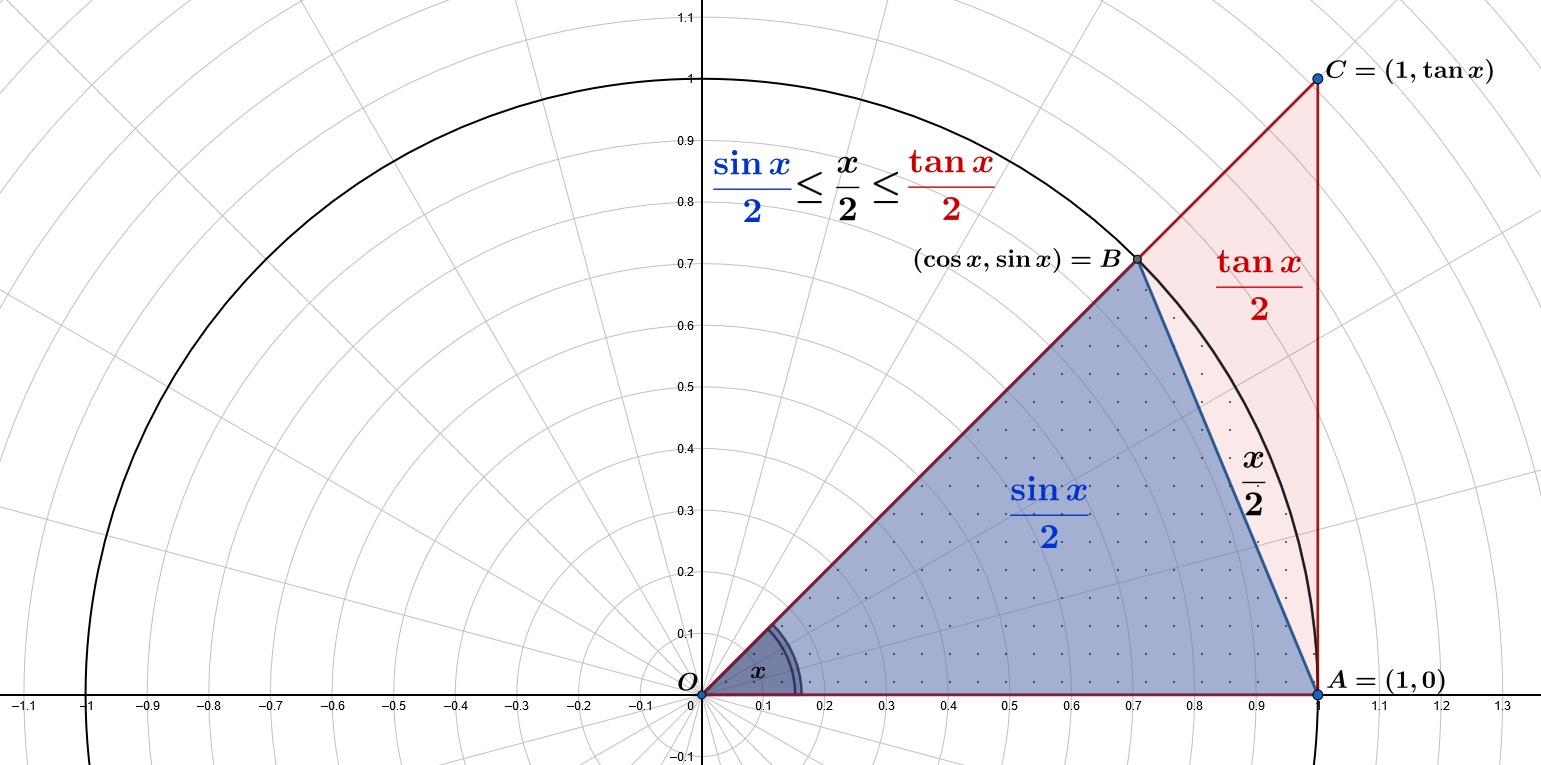
파란색 작은 삼각형 $\color{blue}{OAB}$의 면적은 $\displaystyle A(\color{blue}{OAB})=\frac{1\cdot\sin x}{2}=\color{blue}{\frac{\sin x}{2}}$입니다.
점을 가진 sector의 면적은 $\displaystyle\pi\frac{x}{2\pi}=\frac{x}{2}$입니다.
빨간색 큰 삼각형 $\color{red}{OAC}$의 면적은 $\displaystyle A(\color{red}{OAC})=\frac{1\cdot\tan x}{2}=\color{red}{\frac{\tan x}{2}}$입니다.
그러고 나서 $\displaystyle A(OAB) \leq \frac{x}{2} \leq A(OAC)$라는 관계가 성립합니다:
\[0\lt \sin x \leq x \leq \tan x, \quad\displaystyle\forall x \in ]0, \frac{\pi}{2}[\]$0\lt \sin x$이기 때문에 다음과 같이 쓸 수 있습니다: \(\begin{aligned} \frac{\sin x}{\sin x} &\leq \frac{x}{\sin x} \leq \frac{\tan x}{\sin x}\\ 1&\leq \frac{x}{\sin x} \leq \frac{1}{\cos x}\\ \end{aligned}\)
역수를 취하면:
\[\cos x \leq \frac{\sin x}{x} \leq 1\]$\displaystyle \cos x, \frac{\sin x}{x},1$ 함수가 모두 짝수 함수이므로 다음 결론이 얻어집니다:
\[\quad\cos x \leq \frac{\sin x}{x} \leq 1, \quad \displaystyle\forall x \in ]-\frac{\pi}{2}, 0[ \cup ]0, \frac{\pi}{2}[\]압축 정리를 사용하여: \(\lim _{x \rightarrow 0} \frac{\sin x}{x}= \lim _{x \rightarrow 0} \cos x=\lim _{x \rightarrow 0} 1 = 1\)
따라서 다음 결론이 도출됩니다:
\[\lim _{x \rightarrow 0} \frac{\sin x}{x} = 1\]이 글이나 이 웹사이트가 도움이 되었고 저희 작업을 지원하고 싶다면 기부를 고려해주세요. 감사합니다!
도움 주세요