xが0に近づくと、sin x / xの極限が1であることの証明方法は？

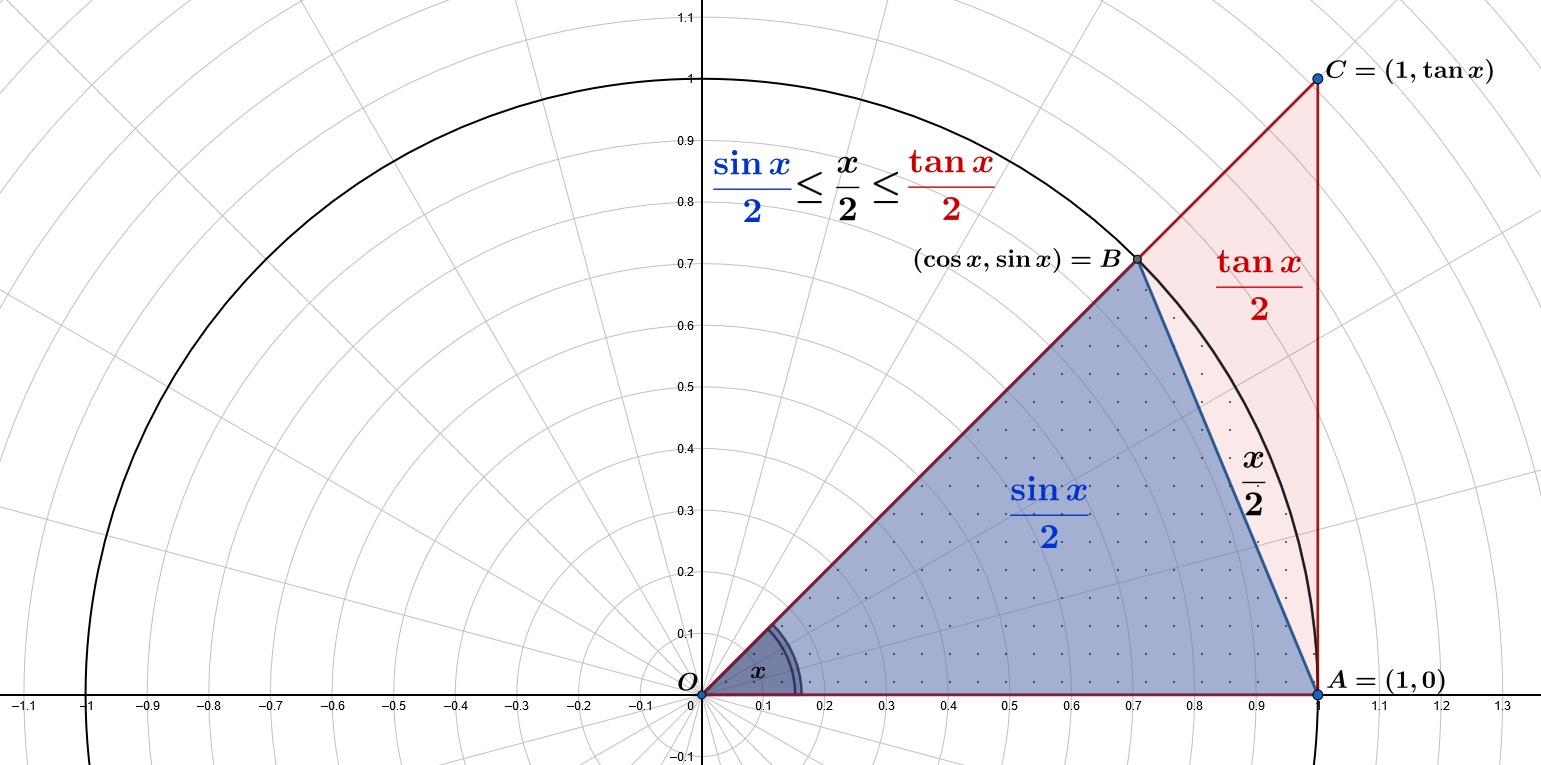
青い小さな三角形$\color{blue}{OAB}$の面積は$\displaystyle A(\color{blue}{OAB})=\frac{1\cdot\sin x}{2}=\color{blue}{\frac{\sin x}{2}}$

点を持つセクターの面積は$\displaystyle\pi\frac{x}{2\pi}=\frac{x}{2}$

赤い大きな三角形$\color{red}{OAC}$の面積は$\displaystyle A(\color{red}{OAC})=\frac{1\cdot\tan x}{2}=\color{red}{\frac{\tan x}{2}}$

その後、$\displaystyle A(OAB) \leq \frac{x}{2} \leq A(OAC)$という関係が成り立ちます：

\[0\lt \sin x \leq x \leq \tan x, \quad\displaystyle\forall x \in ]0, \frac{\pi}{2}[\]

$0\lt \sin x$であるため、次のように書けます： \(\begin{aligned} \frac{\sin x}{\sin x} &\leq \frac{x}{\sin x} \leq \frac{\tan x}{\sin x}\\ 1&\leq \frac{x}{\sin x} \leq \frac{1}{\cos x}\\ \end{aligned}\)

逆数を取ると：

\[\cos x \leq \frac{\sin x}{x} \leq 1\]

$\displaystyle \cos x, \frac{\sin x}{x},1$関数がすべて偶関数であるため、次の結論が得られます：

\[\quad\cos x \leq \frac{\sin x}{x} \leq 1, \quad \displaystyle\forall x \in ]-\frac{\pi}{2}, 0[ \cup ]0, \frac{\pi}{2}[\]

夹逼定理を使用して： \(\lim _{x \rightarrow 0} \frac{\sin x}{x}= \lim _{x \rightarrow 0} \cos x=\lim _{x \rightarrow 0} 1 = 1\)

したがって、次の結論が導かれます：

\[\lim _{x \rightarrow 0} \frac{\sin x}{x} = 1\]