¿Cómo demostrar que límite de sen x / x = 1 cuando x tiende a 0?

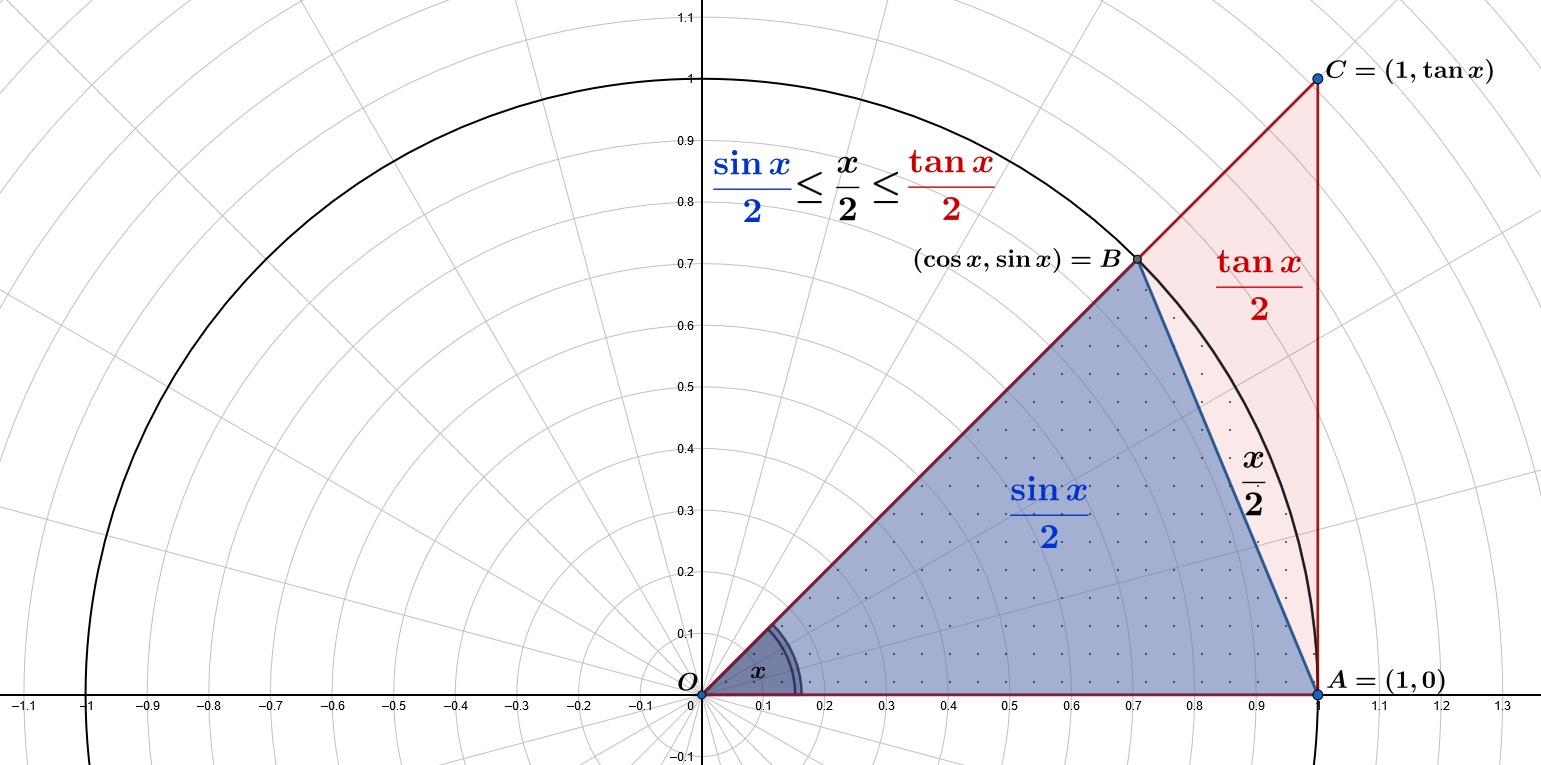
El área del pequeño triángulo azul $\color{blue}{OAB}$ es $\displaystyle A(\color{blue}{OAB})=\frac{1\cdot\operatorname{sen} x}{2}=\color{blue}{\frac{\operatorname{sen} x}{2}}$

El área del sector con puntos es $\displaystyle\pi\frac{x}{2\pi}=\frac{x}{2}$

El área del gran triángulo rojo $\color{red}{OAC}$ es $\displaystyle A(\color{red}{OAC})=\frac{1\cdot\tan x}{2}=\color{red}{\frac{\tan x}{2}}$

Entonces, tenemos $\displaystyle A(\color{blue}{OAB}) \leq \frac{x}{2} \leq A(\color{red}{OAC})$:

\[0\lt \operatorname{sen} x \leq x \leq \tan x, \quad\displaystyle\forall x \in ]0, \frac{\pi}{2}[\]

Ya que $0\lt \operatorname{sen} x$, tenemos

\[\begin{aligned} \frac{\operatorname{sen} x}{\operatorname{sen} x} &\leq \frac{x}{\operatorname{sen} x} \leq \frac{\tan x}{\operatorname{sen} x}\\ 1&\leq \frac{x}{\operatorname{sen} x} \leq \frac{1}{\cos x}\\ \end{aligned}\]

Tomando lo recíproco:

\[\cos x \leq \frac{\operatorname{sen} x}{x} \leq 1\]

Dado que $\displaystyle \cos x, \frac{\operatorname{sen} x}{x},1$ funciones son pares, concluimos que:

\[\quad\cos x \leq \frac{\operatorname{sen} x}{x} \leq 1, \quad \displaystyle\forall x \in ]-\frac{\pi}{2}, 0[ \cup ]0, \frac{\pi}{2}[\]

Usando el teorema del emparedado (teorema del sándwich, teorema del bocadillo o teorema de comparación)

\[\lim _{x \rightarrow 0} \frac{\operatorname{sen} x}{x}= \lim _{x \rightarrow 0} \cos x=\lim _{x \rightarrow 0} 1 = 1\]

Concluímos que:

\[\lim _{x \rightarrow 0} \frac{\operatorname{sen} x}{x} = 1\]