We are going to show that for any angles a, b the trigonometry formula sin (a+b)=sin a cos b + cos a sin b

Proof/Demonstration

Let $(O ; \vec{i}, \vec{j})$ be an orthonormal reference frame, $a$ and $b$ two real numbers defined as follows:

\[\begin{aligned} a&=(\vec{i}, \overrightarrow{O A}) \\ b&=(\overrightarrow{O A}, \overrightarrow{O B}) \end{aligned}\]

Where $A$ and $B$ are the points defined on the trigonometric circle relative to the angles $a$ and $b$.

We then have:

\[a+\frac{\pi}{2}=\left(\vec{i}, \overrightarrow{O A^{\prime}}\right)\]

Where $A^{\prime}$ is the point defined on the trigonometric circle relative to the angle $\displaystyle a+\frac{\pi}{2}$ with $\left(\overrightarrow{O A}, \overrightarrow{O A^{\prime}}\right)=\displaystyle\frac{\pi}{2}$.

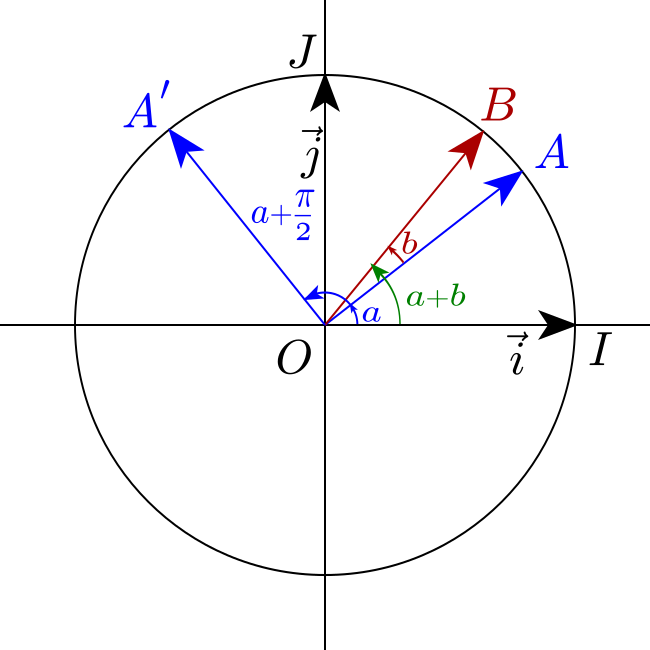
By definition, $\overrightarrow{O A}$ is defined as:

\[\overrightarrow{O A}=\cos a \times \vec{i} + \sin a \times \vec{j}\]

$\overrightarrow{O A^{\prime}}$ is defined as:

\[\overrightarrow{O A^{\prime}}=\cos \left(a+\frac{\pi}{2}\right) \times\vec{i}+\sin \left(a+\frac{\pi}{2}\right) \times\vec{j} = -\sin a \times \vec{i} + \cos a \times \vec{j}\]

$\overrightarrow{O B}$ is defined as:

\[\overrightarrow{O B}=\cos (a+b) \times\vec{i}+\sin (a+b) \times \vec{j}\]

Consider the orthonormal reference frame $\left(O ; \overrightarrow{O A}, \overrightarrow{O A^{\prime}}\right)$. The vector $\overrightarrow{O B}$ in this reference frame is defined as:

\[\begin{aligned} \overrightarrow{O B} &=\cos b \times \overrightarrow{O A} + \sin b \times \overrightarrow{O A^{\prime}} \\ &=\cos b \times (\cos a \times \vec{i} + \sin a \times\vec{j}) + \sin b \times (-\sin a \times\vec{i} + \cos a \times\vec{j}) \\ &=(\cos a \times \cos b-\sin a \times \sin b) \times \vec{i}+(\sin a \times \cos b+\cos a \times \sin b) \times\vec{j} \end{aligned}\]

But we have shown that

\[\overrightarrow{O B}=\cos (a+b) \times\vec{i}+\sin (a+b) \times\vec{j}\]

We obtain by identification: \(\begin{aligned} \cos (a+b)&=\cos a \times \cos b-\sin a \times \sin b \\ \sin (a+b)&=\sin a \times \cos b+\cos a \times \sin b \end{aligned}\)

We have then demonstrated: \(\forall a,b \in \mathbb{R}, \quad \sin (a+b)=\sin a \cos b + \cos a \sin b\)