Nous allons montrer que pour tout élément a, b réels la formule trigonométrique cos (a+b)=cos a cos b - sin a sin b

Soit $(O ; \vec{i}, \vec{j})$ un repère orthonormé, $a$ et $b$ deux réels définis comme suit:

\[\begin{aligned} a&=(\vec{i}, \overrightarrow{O A}) \\ b&=(\overrightarrow{O A}, \overrightarrow{O B}) \end{aligned}\]

où $A$ et $B$ sont les points définis sur le cercle trigonométrique relativement aux angles $a$ et $b$.

On a alors:

\[a+\frac{\pi}{2}=\left(\vec{i}, \overrightarrow{O A^{\prime}}\right)\]

où $A^{\prime}$ est le point défini sur le cercle trigonométrique relativement à l’angle $\displaystyle a+\frac{\pi}{2}$ avec $\left(\overrightarrow{O A}, \overrightarrow{O A^{\prime}}\right)=\displaystyle\frac{\pi}{2}$.

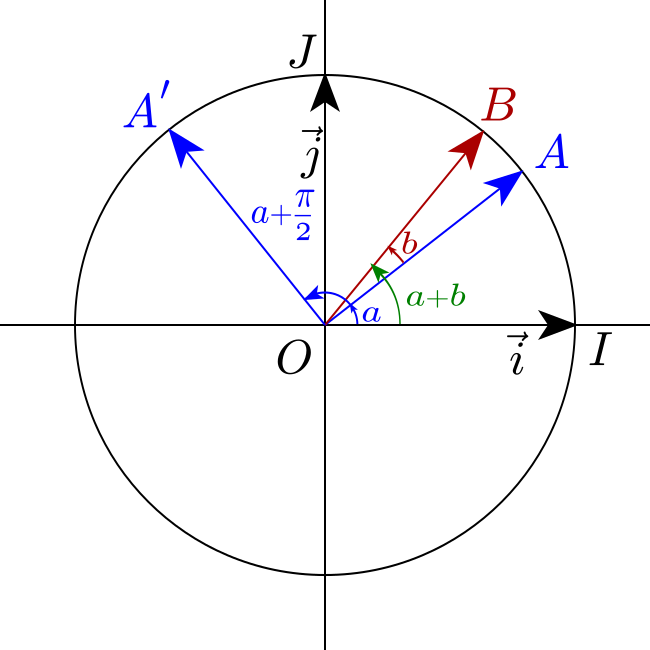
Par définition, $\overrightarrow{O A}$ est définir par:

\[\overrightarrow{O A}=\cos a \times \vec{i} + \sin a \times \vec{j}\]

$\overrightarrow{O A^{\prime}}$ est définir par:

\[\overrightarrow{O A^{\prime}}=\cos \left(a+\frac{\pi}{2}\right) \times\vec{i}+\sin \left(a+\frac{\pi}{2}\right) \times\vec{j} = -\sin a \times \vec{i} + \cos a \times \vec{j}\]

$\overrightarrow{O B}$ est définir par:

\[\overrightarrow{O B}=\cos (a+b) \times\vec{i}+\sin (a+b) \times \vec{j}\]

Considérons le repère orthonormé $\left(O ; \overrightarrow{O A}, \overrightarrow{O A^{\prime}}\right)$. Le vecteur $\overrightarrow{O B}$ dans ce repère est définir par:

\[\begin{aligned} \overrightarrow{O B} &=\cos b \times \overrightarrow{O A} + \sin b \times \overrightarrow{O A^{\prime}} \\ &=\cos b \times (\cos a \times \vec{i} + \sin a \times\vec{j}) + \sin b \times (-\sin a \times\vec{i} + \cos a \times\vec{j}) \\ &=(\cos a \times \cos b-\sin a \times \sin b) \times \vec{i}+(\sin a \times \cos b+\cos a \times \sin b) \times\vec{j} \end{aligned}\]

Mais nous avons montré que

\[\overrightarrow{O B}=\cos (a+b) \times\vec{i}+\sin (a+b) \times\vec{j}\]

On obtient alors par identification: \(\begin{aligned} \cos (a+b)&=\cos a \times \cos b-\sin a \times \sin b \\ \sin (a+b)&=\sin a \times \cos b+\cos a \times \sin b \end{aligned}\)

On a alors démontré: \(\forall a,b \in \mathbb{R}, \quad \cos (a+b)=\cos a \cos b-\sin a \sin b\)