Math-Linux.com
Knowledge base dedicated to Linux and applied mathematics.
Accueil > Mathématiques > Trigonométrie > La fonction cosinus est paire cos(-x)=cos x
La fonction cosinus est paire cos(-x)=cos x
Toutes les versions de cet article : <English> <français>
On démontre ici que la fonction cosinux cos(-x)=cos x est paire géométriquement à l’aide du cercle unitaire.
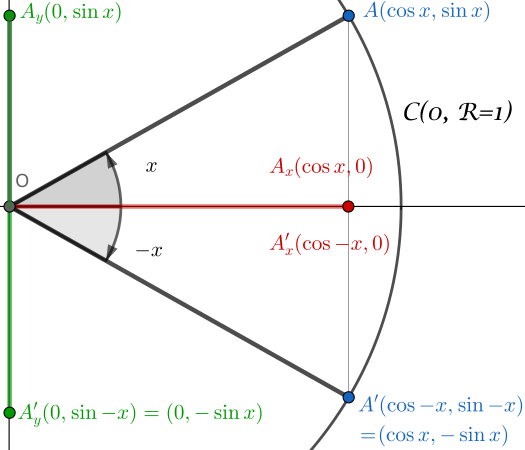
On se met dans la configuration suivante :
– cercle unitaire $\mathcal{C}(O,R=1)$
– définition de l’angle $x$
– définition de l’angle $-x$
Considérez alors les triangles respectifs : $(OA_xA)$ et $(OA’_xA’)$.
Preuve/démonstration que cosinus est paire cos(-x) = cos (x)
Prenez la définition respective des cosinus des angles $x$ et $-x$.
Dans le triangle $(OA_xA)$ :
$$ \cos x=\frac{\textrm{adjacent}}{\textrm{hypotenuse}}=\frac{|OA_x|}{R}=\frac{|OA_x|}{1}=|OA_x| $$
Dans le triangle $(OA’_xA’)$ :
$$ \cos (-x)=\frac{\textrm{adjacent}}{\textrm{hypotenuse}}=\frac{|OA’_x|}{R}=\frac{|OA’_x|}{1}=|OA’_x| $$
Or, puisque par construction on a $|OA_x|= |OA’_x|$, on retrouve que :
$$ \forall x\in \mathbb{R},\quad : \cos (-x)=\cos x $$
Dans la même rubrique
- Démonstration / preuve de cos²x + sin²x=1
- Formule addition cos(a+b)=cos a cos b - sin a sin b
- Formule addition cosh(x + y) = cosh x cosh y +sinh x sinh y
- Formule addition cosh(x - y) = cosh x cosh y - sinh x sinh y
- Formule addition sin(a+b)=sin a cos b + cos a sin b
- Formule addition sinh(x + y) = sinh x cosh y +cosh x sinh y
- Formule addition sinh(x - y) = sinh x cosh y - cosh x sinh y
- Formule trigonométrique cos(a-b)=cos a cos b + sin a sin b
- Formule trigonométrique sin(2x)=2 sin x cos x
- Formule trigonométrique sin(a-b)=sin a cos b - sin b cos a
- La fonction cosinus est paire cos(-x)=cos x
- La fonction sinus est impaire sin(-x)=-sin x
- La fonction tangente est impaire tan(-x)=-tan x