Demonstramos que a função seno sin(-x)=-sin x é ímpar geometricamente usando o círculo unitário.

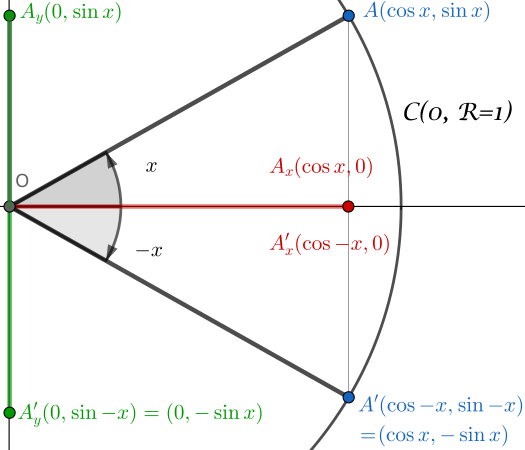
Estamos na seguinte configuração:

  • Círculo unitário $\mathcal{C}(O,R=1)$
  • Definição do ângulo $x$
  • Definição do ângulo $-x$

Considere então os triângulos respectivos: $(OA_xA)$ e $(OA’_xA’)$.

Demonstração de que o seno é uma função ímpar sin(-x) = -sin (x)

Vamos considerar as definições respectivas dos senos dos ângulos $x$ e $-x$.

No triângulo $(OA_xA)$:

\[\operatorname{sen} x=\frac{\textrm{cateto oposto}}{\textrm{hipotenusa}}=\frac{|OA_y|}{R}=\frac{|OA_y|}{1}=|OA_y|\]

No triângulo $(OA’_xA’)$:

\[\operatorname{sen} (-x)=\frac{\textrm{cateto oposto}}{\textrm{hipotenusa}}=\frac{|OA'_y|}{R}=\frac{|OA'_y|}{1}=|OA'_y|\]

Agora, dado que por construção temos $\vert OA_y\vert= -\vert OA’_y\vert$, obtemos:

\[\forall x\in \mathbb{R},\quad: \operatorname{sen} (-x)=-\operatorname{sen} x\]

Isso mostra que a função seno é ímpar, pois ela satisfaz a propriedade $\sin(-x) = -\sin(x)$.