我们在这里证明正弦函数 sin (-x) = - sin x 是奇函数，使用单位圆。

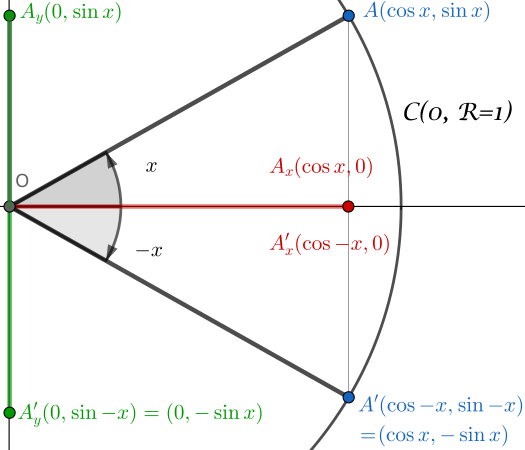
我们从以下配置开始：

  • 单位圆 $\mathcal{C}(O,R=1)$
  • 角度 $x$ 的定义
  • 角度 $-x$ 的定义

现在考虑三角形：$(OA_xA)$ 和 $(OA’_xA’)$。

正弦函数是奇函数 sin(-x) = -sin (x) 的证明

取角度 $x$ 和 $-x$ 的正弦函数的定义。

在三角形 $(OA_xA)$ 中：

\[\sin x=\frac{\textrm{对边}}{\textrm{斜边}}=\frac{\vert OA_y\vert }{R}=\frac{\vert OA_y\vert }{1}=\vert OA_y\vert\]

在三角形 $(OA’_xA’)$ 中：

\[\sin (-x)=\frac{\textrm{对边}}{\textrm{斜边}}=\frac{\vert OA'_y\vert }{R}=\frac{\vert OA'_y\vert }{1}=\vert OA'_y\vert\]

根据构造：$\vert OA_y\vert = -\vert OA’_y\vert $，因此我们有

\[\forall x\in \mathbb{R},\quad: \sin (-x)=-\sin x\]