الجيب تابع للجيب sin(-x)=-sin x

نثبت هنا أن الجيب تابع للجيب sin(-x)=-sin x هو تابع جفري هندسيًا باستخدام الدائرة الوحدية.

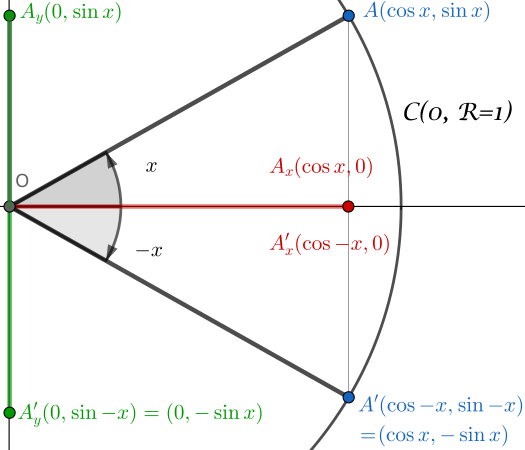
نجد أنفسنا في التكوين التالي:

• الدائرة الوحدية $\mathcal{C}(O,R=1)$
• تعريف زاوية $x$
• تعريف زاوية $-x$

لننظر إذا في المثلثين المقابلين: $(OA_xA)$ و $(OA’_xA’)$.

دليل أن الجيب تابع للجيب sin(-x) = -sin (x)

لنأخذ التعاريف المقابلة لقيم الجيب للزوايا $x$ و $-x$.

في المثلث $(OA_xA)$:

\[\sin x=\frac{\textrm{الضلع المقابل}}{\textrm{الوتر}}=\frac{|OA_y|}{R}=\frac{|OA_y|}{1}=|OA_y|\]

في المثلث $(OA’_xA’)$:

\[\sin (-x)=\frac{\textrm{الضلع المقابل}}{\textrm{الوتر}}=\frac{|OA'_y|}{R}=\frac{|OA'_y|}{1}=|OA'_y|\]

الآن، نظرًا لأنه بناءً على البنية لدينا $\vert OA_y\vert= -\vert OA’_y\vert$، فإننا نحصل على:

\[\forall x\in \mathbb{R},\quad: \sin (-x)=-\sin x\]

هذا يظهر أن الجيب تابع للجيب هو تابع جفري، حيث يتوافق مع الخاصية

\[\sin(-x) = -\sin(x)\]