Wir zeigen hier, dass die Sinusfunktion sin(-x)=-sin x geometrisch ungerade ist, indem wir den Einheitskreis verwenden.

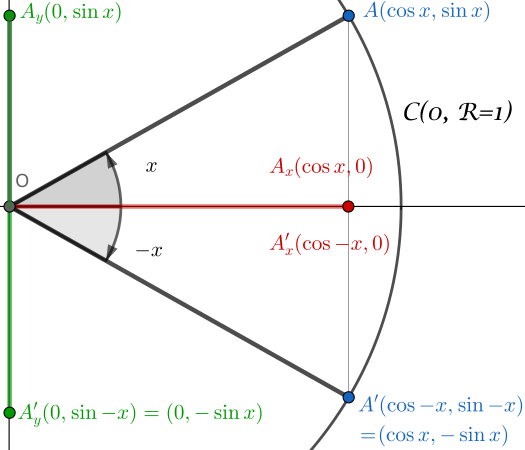
Wir befinden uns in folgender Konfiguration:

  • Einheitskreis $\mathcal{C}(O,R=1)$
  • Definition des Winkels $x$
  • Definition des Winkels $-x$

Betrachten Sie dann die jeweiligen Dreiecke: $(OA_xA)$ und $(OA’_xA’)$.

Beweis, dass der Sinus eine ungerade Funktion ist sin(-x) = -sin (x)

Nehmen Sie die jeweiligen Definitionen der Sinuswerte der Winkel $x$ und $-x$.

Im Dreieck $(OA_xA)$:

\[\sin x=\frac{\textrm{Gegenkathete}}{\textrm{Hypotenuse}}=\frac{|OA_y|}{R}=\frac{|OA_y|}{1}=|OA_y|\]

Im Dreieck $(OA’_xA’)$:

\[\sin (-x)=\frac{\textrm{Gegenkathete}}{\textrm{Hypotenuse}}=\frac{|OA'_y|}{R}=\frac{|OA'_y|}{1}=|OA'_y|\]

Da wir aufgrund der Konstruktion haben, dass $\vert OA_y\vert= -\vert OA’_y\vert$, erhalten wir:

\[\forall x\in \mathbb{R},\quad: \sin (-x)=-\sin x\]

Dies zeigt, dass die Sinusfunktion ungerade ist, da sie die Eigenschaft

\[\sin(-x) = -\sin(x)\]

erfüllt.