Dimostriamo qui che la funzione seno sin(-x)=-sin x è dispari geometricamente utilizzando il cercle unitario.

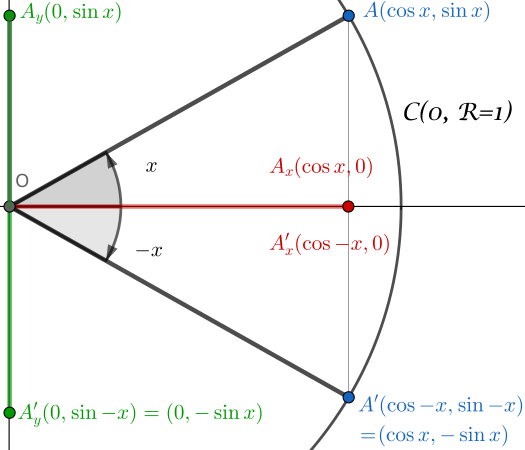
Ci troviamo nella seguente configurazione:

  • cercle unitario $\mathcal{C}(O,R=1)$
  • definizione dell’angolo $x$
  • definizione dell’angolo $-x$

Consideriamo quindi i rispettivi triangoli: $(OA_xA)$ e $(OA’_xA’)$.

Dimostrazione che il seno è una funzione dispari sin(-x) = -sin (x)

Prendiamo le definizioni rispettive dei seni degli angoli $x$ e $-x$.

Nel triangolo $(OA_xA)$:

\[\sin x=\frac{\textrm{opposto}}{\textrm{ipotenusa}}=\frac{|OA_y|}{R}=\frac{|OA_y|}{1}=|OA_y|\]

Nel triangolo $(OA’_xA’)$:

\[\sin (-x)=\frac{\textrm{opposto}}{\textrm{ipotenusa}}=\frac{|OA'_y|}{R}=\frac{|OA'_y|}{1}=|OA'_y|\]

Ora, dato che per costruzione abbiamo $\vert OA_y\vert= -\vert OA’_y\vert$, otteniamo:

\[\forall x\in \mathbb{R},\quad: \sin (-x)=-\sin x\]