Demostramos que la función seno sen(-x)=-sen x es impar geométricamente utilizando el círculo unitario.

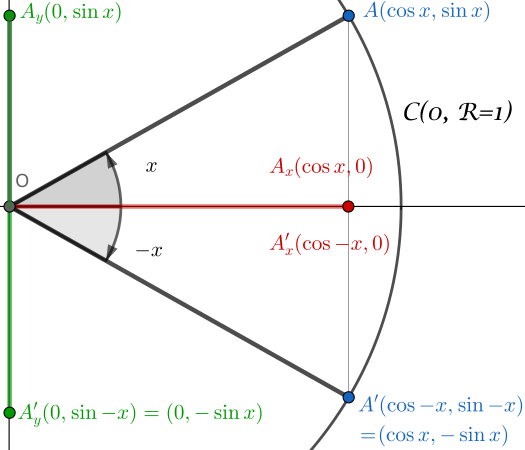
Nos encontramos en la siguiente configuración:

  • círculo unitario $\mathcal{C}(O,R=1)$
  • definición del ángulo $x$
  • definición del ángulo $-x$

Consideramos entonces los triángulos respectivos: $(OA_xA)$ y $(OA’_xA’)$.

Demostración de que el seno sen es una función impar sen(-x) = -sen(x)

Tomamos las definiciones respectivas del seno \operatorname{sen} de los ángulos $x$ y $-x$.

En el triángulo $(OA_xA)$:

\[\operatorname{sen} x=\frac{\textrm{opuesto}}{\textrm{hipotenusa}}=\frac{|OA_y|}{R}=\frac{|OA_y|}{1}=|OA_y|\]

En el triángulo $(OA’_xA’)$:

\[\operatorname{sen} (-x)=\frac{\textrm{opuesto}}{\textrm{hipotenusa}}=\frac{|OA'_y|}{R}=\frac{|OA'_y|}{1}=|OA'_y|\]

Ahora, dado que por construcción tenemos $\vert OA_y\vert= -\vert OA’_y\vert$, obtenemos:

\[\forall x\in \mathbb{R},\quad: \operatorname{sen} (-x)=-\operatorname{sen} x\]