Синус-функция является нечетной sin(-x)=-sin x

Мы докажем, что синус-функция sin(-x)=-sin x является геометрически нечетной, используя единичную окружность.

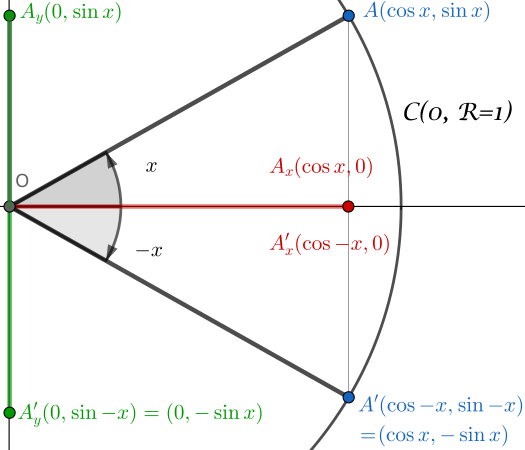
Мы находимся в следующей конфигурации:

• Единичная окружность $\mathcal{C}(O,R=1)$
• Определение угла $x$
• Определение угла $-x$

Рассмотрим соответствующие треугольники: $(O{A}_{x}A)$ и $(O{A}_x^{\prime }{A}^{\prime })$.

Доказательство того, что синус-функция является нечетной sin(-x) = -sin (x)

Примем соответствующие определения синусов углов $x$ и $-x$.

В треугольнике $(O{A}_{x}A)$:

$$\sin x=\frac{\text{противоположный катет}}{\text{гипотенуза}}=\frac{|O{A}_y|}{R}=\frac{|O{A}_y|}{1}=|O{A}_y|$$

В треугольнике $(O{A}_x^{\prime }{A}^{\prime })$:

$$\sin (-x)=\frac{\text{противоположный катет}}{\text{гипотенуза}}=\frac{|O{A}_y^{\prime }|}{R}=\frac{|O{A}_y^{\prime }|}{1}=|O{A}_y^{\prime }|$$

Так как по конструкции мы имеем $|O{A}_y|=-|O{A}_y^{\prime }|$, мы получаем:

$$\mathrm{\forall }x\in \mathbb{R},:\sin (-x)=-\sin x$$

Это показывает, что синус-функция является нечетной, так как она удовлетворяет свойству

$$\sin (-x)=-\sin (x)$$