साइन एक विषम फ़ंक्शन है sin(-x)=-sin x
हम यहां सिखेंगे कि साइन फ़ंक्शन sin (-x) = -sin x विषम है, इकाई वृत्त का उपयोग करके।
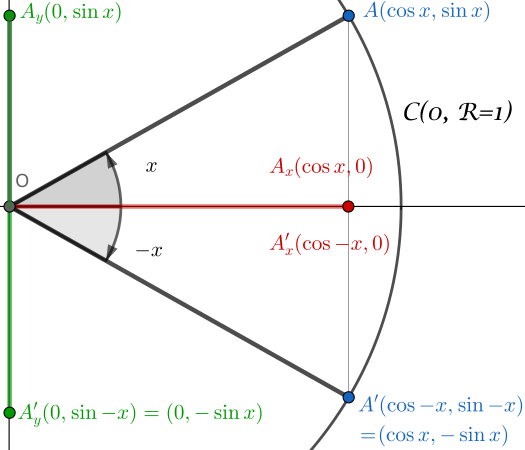
हम निम्नलिखित विन्यास के साथ शुरू करते हैं:
- यूनिट सर्कल $\mathcal{C}(O,R=1)$
- कोण $x$ की परिभाषा
- कोण $-x$ की परिभाषा
अब त्रिभुजों को विचार करें: $(OA_xA)$ और $(OA’_xA’)$।
साइन एक विषम फ़ंक्शन है sin(-x) = -sin (x)
कोणों $x$ और $-x$ के साइनों की परिभाषा लें।
त्रिभुज $(OA_xA)$ में:
\[\sin x = \frac{\textrm{विपरीत}}{\textrm{विकेन्द्र}} = \frac{\vert OA_y\vert}{R} = \frac{\vert OA_y\vert}{1} = \vert OA_y\vert\]त्रिभुज $(OA’_xA’)$ में:
\[\sin (-x) = \frac{\textrm{विपरीत}}{\textrm{हाइपोटेनुस}} = \frac{\vert OA'_y\vert}{R} = \frac{\vert OA'_y\vert}{1} = \vert OA'_y\vert\]निर्माण के आधार पर: $\vert OA_y\vert = -\vert OA’_y\vert $, तो हमारे पास है
\[\forall x\in \mathbb{R},\quad: \sin (-x) = -\sin x\]अगर आपको यह पोस्ट या इस वेबसाइट से सहायक मिला और हमारे काम का समर्थन करना चाहते हैं, तो कृपया एक दान करने की सोचें। धन्यवाद!
हमें मदद करें