সাইন একটি বিজোড় ফাংশন sin(-x)=-sin x
এখানে আমরা এই সিন ফাংশন sin (-x) = -sin x যে বিজোড় তা উপযুক্ত একটি বিজোড় সত্যাপন করি, একক বৃত্ত ব্যবহার করে।
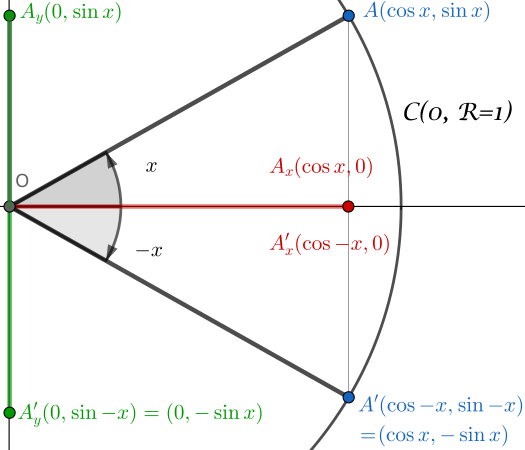
আমরা নিম্নলিখিত কনফিগারেশন দিয়ে শুরু করি:
- একক বৃত্ত $\mathcal{C}(O,R=1)$
- কোণ $x$ এর সংজ্ঞা
- কোণ $-x$ এর সংজ্ঞা
এখন চিন্তা করুন: $(OA_xA)$ এবং $(OA’_xA’)$ ত্রিভুজ।
সিন একটি বিজোড় ফাংশন sin(-x) = -sin (x) এর প্রমাণ
কোণ $x$ এবং $-x$ এর সাইনের সংজ্ঞা নিন।
ত্রিভুজ $(OA_xA)$ এ:
\[\sin x=\frac{\textrm{পার্শ্ব}}{\textrm{উপত্যকা}}=\frac{\vert OA_y\vert}{R}=\frac{\vert OA_y\vert}{1}=\vert OA_y\vert\]ত্রিভুজ $(OA’_xA’)$ এ:
\[\sin (-x)=\frac{\textrm{পার্শ্ব}}{\textrm{উপত্যকা}}=\frac{\vert OA'_y\vert}{R}=\frac{\vert OA'_y\vert}{1}=\vert OA'_y\vert\]নির্মাণ দ্বারা: $\vert OA_y\vert = -\vert OA’_y\vert $, তাহলে আমরা নিশ্চিত হই:
\[\forall x\in \mathbb{R},\quad: \sin (-x)=-\sin x\]আপনি যদি এই পোস্ট বা এই ওয়েবসাইট সাহায্যকর পেতেন এবং আমাদের কাজে সাহায্য করতে চান তবে দয়া করে একটি দান করতে চিন্তা করুন। ধন্যবাদ!
আমাদের সাহায্য করুন