この記事では、単位円を使用して、正弦関数 sin (-x) = - sin x が奇関数であることを証明します。

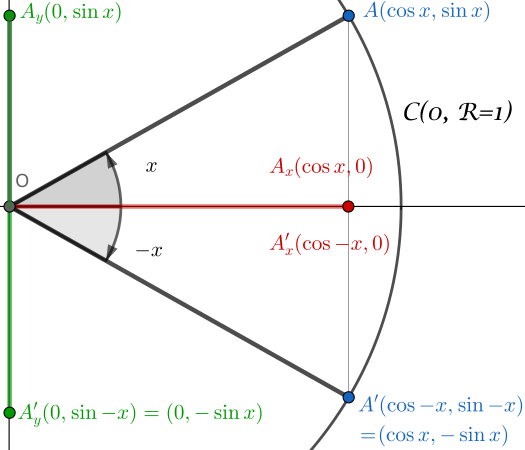
以下の設定から始めます：

  • 単位円 $\mathcal{C}(O,R=1)$
  • 角 $x$ の定義
  • 角 $-x$ の定義

さて、三角形 $(OA_xA)$ と $(OA’_xA’)$ を考えてみましょう。

正弦が奇関数 sin(-x) = -sin (x) であることの証明

角 $x$ と $-x$ の正弦の定義を考えましょう。

三角形 $(OA_xA)$ では：

\[\sin x=\frac{\textrm{対辺}}{\textrm{斜辺}}=\frac{\vert OA_y\vert}{R}=\frac{\vert OA_y\vert}{1}=\vert OA_y\vert\]

三角形 $(OA’_xA’)$ では：

\[\sin (-x)=\frac{\textrm{対辺}}{\textrm{斜辺}}=\frac{\vert OA'_y\vert}{R}=\frac{\vert OA'_y\vert}{1}=\vert OA'_y\vert\]

建設により、$\vert OA_y\vert = -\vert OA’_y\vert $ となるので、次が成り立ちます：

\[\forall x\in \mathbb{R},\quad: \sin (-x) = -\sin x\]