이 문서에서는 단위 원을 이용하여 정현함수 sin (-x) = - sin x가 홀함수임을 증명합니다.

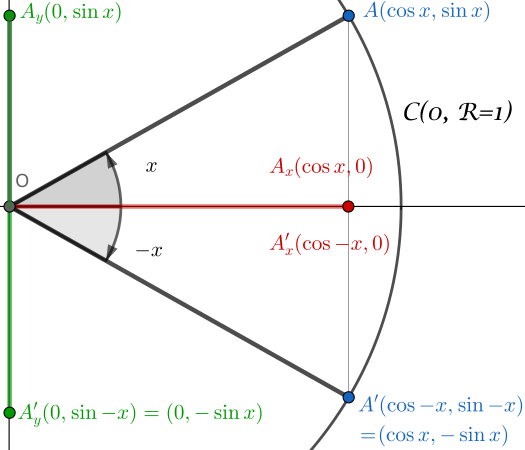
다음과 같은 설정에서 시작합니다:

  • 단위 원 $\mathcal(C)(O, R=1)$
  • 각 $x$의 정의
  • 각 $-x$의 정의

이제 삼각형 $(OA_xA)$와 $(OA’_xA’)$를 고려해 봅시다.

정현함수가 홀함수 sin(-x) = -sin (x)임을 증명

각 $x$와 $-x$의 정의를 살펴봅시다.

삼각형 $(OA_xA)$에서:

\[\sin x=\frac{맞은편}{빗변}=\frac{\vert OA_y\vert}{R}=\frac{\vert OA_y\vert}{1}=\vert OA_y\vert\]

삼각형 $(OA’_xA’)$에서:

\[\sin (-x)=\frac{맞은편}{빗변}=\frac{\vert OA'_y\vert}{R}=\frac{\vert OA'_y\vert}{1}=\vert OA'_y\vert\]

건설에 의해 $\vert OA_y\vert = -\vert OA’_y\vert$가 되므로 다음이 성립합니다:

\[\forall x\in \mathbb{R},\quad: \sin (-x) = -\sin x\]